未来技术学院 2021 级选拔考试(数学)模拟样题
考前须知
- 根据阅读材料,完成后面的 5 道题,时长共计 2 个小时;
- 本试题由往届学长根据 2018 级、2019 级、2020 级求是数学选拔考试试题,及 2020 级求是学部选拔考试(数学部分)的考场回忆编写的样题。本题只具有题目形式的参考意义,既不代表最终难度,也不代表实际考试内容,更不代表求是学部,和数学学院。请谨慎看待这张试题难度,题型以及内容;
- 本试题为大学课程内容随机摘选,若有纰漏请与笔者联系,望周知;
- 试题适用范围:求是学部,求是数学班选拔考试;
不适用范围:腾讯新工科试验班,化工学院领军计划,精仪工程科学班
阅读材料
定义 1 依赖于参数(一般情况下为时间$t$)的一组随机变量的全体称为随机过程,也就是对于任意的 $t \in T$,每个时间点$t$都能找到对应的随机变量$X(t)$,则对于这一系列的t对应的一族随机变量我们称为随机过程。记为
$$\{ X(t), t \in T \} \qquad (1-1)$$
$X(t)$ 称为$t$时刻的状态,$X(t)$所有可能的取值称为状态空间, 如果状态空间的所有可能取值均在有限集内,或无限可数集内,则称上述过程为离散时间随机过程
定义2 如果对于任意的正整数$n$及任意$n$个不同的$t_{1}, t_{2}, t_{3}, \cdots, t_{n} \in T$, 随机变量$X(t_{1}), X(t_{2}), \cdots, X(t_{n})$均互相独立,则称$\{ X(t), t \in T \}$为独立过程
定义3对于随机过程$\{ X(t), t \in T \}$,如果对于任意给定的参数$t_{1} < t_{2} < \cdots < t_{n}$总有
$$P(X(t_{n}) \leq x_{n} | X(t_{1})=x_{1},X(t_{2})=x_{2}, \cdots, X(t_{n-1})=x_{n-1})=P(X(t_{n}) \leq x_{n} | X(t_{n-1})=x_{n-1}), (1-2)$$
则称其满足马尔可夫性质,称这一随机过程为马尔可夫过程。更严格的,对于离散时间随机过程,则马尔可夫性质亦满足等式
$$P(X(t_{n}) = x_{n} | X(t_{1})=x_{1},X(t_{2})=x_{2}, \cdots, X(t_{n-1})=x_{n-1})=P(X(t_{n}) = x_{n} | X(t_{n-1})=x_{n-1}), (1-3) $$
其中$P(X(t_{n}) = x_{n} | X(t_{n-1})=x_{n-1})$为由状态$ X(t_{n-1})$到$X(t_n)$的转移概率(下简称为转移概率),满足上述性质(1-3)的离散时间随机过程又称马尔可夫链。
马尔可夫性质是对于历史和过于未来随机状态的描述,它反映了下一时刻的状态仅与当前状态有关,而与上一时刻状态无关,因此又被称为无后效性。
定义4 若转移概率$P(X(t_{n}) = x_{n} | X(t_{n-1})=x_{n-1})$与$n$无关,则称该马尔可夫链为齐次马尔可夫链,否则为非齐次马尔可夫链(后文如无必要说明,仅考虑齐次马尔可夫链)。
例1 独立随机过程是马尔可夫过程
证明:
对于任意的$t_{1}, t_{2}, t_{3}, \cdots, t_{n} \in T$,因$X(t_{1}), X(t_{2}), \cdots, X(t_{n})$均互相独立,则有
$$P(X(t_{n}) \leq x_{n} | X(t_{1})=x_{1},X(t_{2})=x_{2}, \cdots, X(t_{n-1})=x_{n-1})$$
$$=\dfrac{P(X(t_{n}) \leq x_{n}, X(t_{1})=x_{1},X(t_{2})=x_{2}, \cdots, X(t_{n-1})=x_{n-1})}{P(X(t_{1})=x_{1},X(t_{2})=x_{2}, \cdots, X(t_{n-1})=x_{n-1})}$$
$$=\dfrac{P(X(t_{n}) \leq x_{n})P(X(t_{1})=x_{1})P(X(t_{2})=x_{2}) \cdots P( X(t_{n-1})=x_{n-1})}{P(X(t_{1})=x_{1})P(X(t_{2})=x_{2}) \cdots P(X(t_{n-1})=x_{n-1})}$$
$$=P(X(t_{n}) \leq x_{n})=P(X(t_{n}) \leq x_{n} | X(t_{n-1})=x_{n-1})$$
例2设随机过程$\{ X_{n}, n \geq 1 \}$,$X_{n}$是第$n$次投掷一颗骰子的点数,则该过程为马尔可夫过程
定义4记马尔可夫链中由状态$X_{n-1}=i$到状态$X_{n}=j$的转移概率为$p_{ij}$,则由状态空间内所有转移概率构成的矩形数表,形如
$$P=\begin{bmatrix} p_{11}&p_{12}&p_{13}&\cdots&p_{1j}&\cdots \\ p_{21}&p_{22}&p_{23}&\cdots&p_{2j}&\cdots \\ p_{31}&p_{32}&p_{33}&\cdots&p_{3j}&\cdots \\ \vdots&\vdots&\vdots&\ddots&\vdots&\ddots\\ p_{i1}&p_{i2}&p_{i3}&\cdots&p_{ij}&\cdots \\ \vdots&\vdots&\vdots&\ddots&\vdots&\ddots\end{bmatrix}$$
称为转移概率矩阵$P$。其中第$i$行,第$j$个元素即表示$p_{ij}$, 易知$p_{ij} \geq 0$, $\sum\limits_{j=0}^{\infty}p_{ij}=1$
记随机过程$\{X_{n}, n \geq 1\}$中状态$X_{n-1}$到状态$X_{n}$的转移矩阵为$P(1)$,又称一步转移概率矩阵,
状态$X_{n-1}$到状态$X_{n+1}$的转移概率矩阵为$P(2)$,又称二步转移概率矩阵,以此类推。另外有,状态$X_{n}=i$到状态$X_{n+m}=j$的转移概率为$p_{ij}(m)$。
例3 设任意相连的两天中,雨天转晴天的概率为$\dfrac{1}{3}$, 晴天转雨天的概率为$\dfrac{1}{2}$,任意一天晴或雨互为逆事件。以0表示晴天状态,以1表示雨天状态, $X_{n}$表示第$n$天的状态。试求马尔可夫链$\{ X_{n}, n \geq 1 \}$的一步转移概率矩阵,又已知5月1日为晴天,问5月3日为晴天的概率为多少?
解:状态空间为$\{0,1\}$,由根据题意,晴天和雨天互为逆事件。则有转移概率有$p_{00}=\dfrac{1}{2}, p_{01}=\dfrac{1}{2}, p_{10}=\dfrac{1}{3}, p_{11}=\dfrac{2}{3}$
故一步转移概率矩阵为
$$P=\begin{bmatrix} \dfrac{1}{2}&\dfrac{1}{2}\\ \dfrac{1}{3}&\dfrac{2}{3}\end{bmatrix}$$
$p_{00}(2)=1/2 \times 1/2 + 1/2 \times 1/3=5/12$,5月3日晴天概率为$5/12$
定义5描述状态空间内转移概率及关系的指向图又称状态转移图。
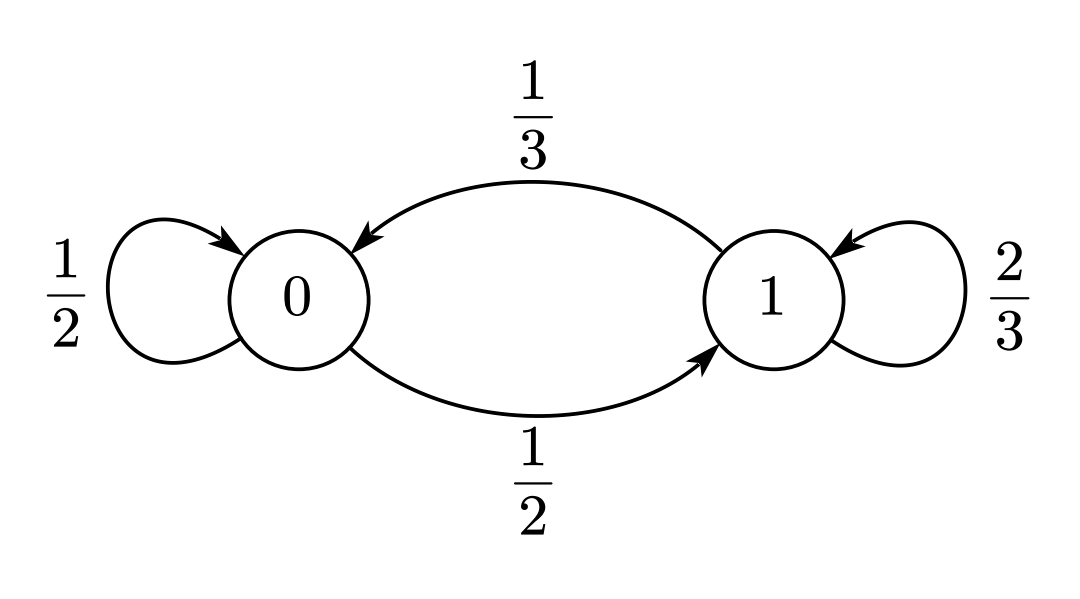
例4例3中的状态转移图如下图所示,其中圆圈内的0,和1分别表示状态0和状态1,箭头所指和其所对应的数字分别表示由某一状态转到另一相同/不同状态的转移概率。如由状态0指向状态1的箭头表示由状态0转移到状态1的概率为1/2;相应地,由状态0指向自身的箭头表示由状态0转移到状态0的概率为1/2。状态1同理。
定义6 对于状态空间$S$中的某一状态$k$,如果对任意的$j \in S, j \neq k$均有$p_{kk}=1, p_{kj}=0$,则称状态$k$为吸收态
定义7记$f_{ij}(n)=P(X_{m+v} \neq j, 1 \leq v \leq n-1, X_{m+n}=j|X_m=i),n\geq 1$,即状态空间中的状态$i$出发,经$n$步首次到达$j$的概率,称为首中概率。另记$f_{ij}=\sum\limits_{n=1}^{\infty}f_{ij}(n)$, 它指经状态$i$出发,经有限步终于到达状态$j$的概率。
定义8 对于状态空间中的某一状态$i$,若$f_{ii}=1$,则称该状态是常返态;如果$f_{ii}<1$,则称该状态是非常返态;
定理1 状态$i$是常返态的充要条件是$\sum\limits_{n=0}^{\infty}p_{ii}(n)=\infty$
状态$i$是非常返态的充要条件是$\sum\limits_{n=0}^{\infty}p_{ii}(n)<\infty$(证略)
命题1 如果状态$j$是非常返态,则对于状态空间中任意状态$i$,均有$\lim\limits_{n \to +\infty}p_{ij}(n)=0$(证略)
定理2 如果$f_{ij} > 0$且,$f_{ji}<1$,则$i$是常返态(证略)
试卷题目(每题 20 分,满分 100 分)
一、设有三个黑球和三个白球,把这六个球分给甲乙两人各三个球,并把甲拥有的白球数定义为该过程的状态,则有四种状态$0,1,2,3$。现每次从甲乙双方各取一球,然后相互交换。经过$n$次交换后过程的状态记为$X_{n}(n \geq 1)$,试说明该过程是马尔可夫过程,并求一步转移概率矩阵$P(1)$,画出状态转移图。
二.设有任意元素均为实数的两行两列矩阵$A$, $B$ $$A=\begin{bmatrix} a_{11}&a_{12}\\ a_{21}&a_{22}\end{bmatrix}$$ $$B=\begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\end{bmatrix}$$ 定义乘法运算 $$A \times B=\begin{bmatrix} a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\ a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22} \end{bmatrix}$$ 又定义矩阵乘方运算$A^n=A\times A \times A \cdots A$($n$个$A$相乘),求证:对于状态空间内仅有两个元素$\{0,1\}$马尔可夫链的转移概率矩阵$P$
(1)$P^2=P(2)$
(2)$P^n=P(n)$
三、设随机过程$\{ X_{n}, n \geq 1 \}$,$X_{n}$是第$n$次投掷一枚硬币的结果,正面为状态1,反面为状态0。试证明状态1,和状态0均为常返态
四、某学生由在校状态分别有如下七种,玩手机,听课程1,听课程2, 听课程3, 通过考试,去社团活动,睡觉,定义这七种状态分别为$0, 1, 2, 3, 4, 5, 6$。状态转移图如下。
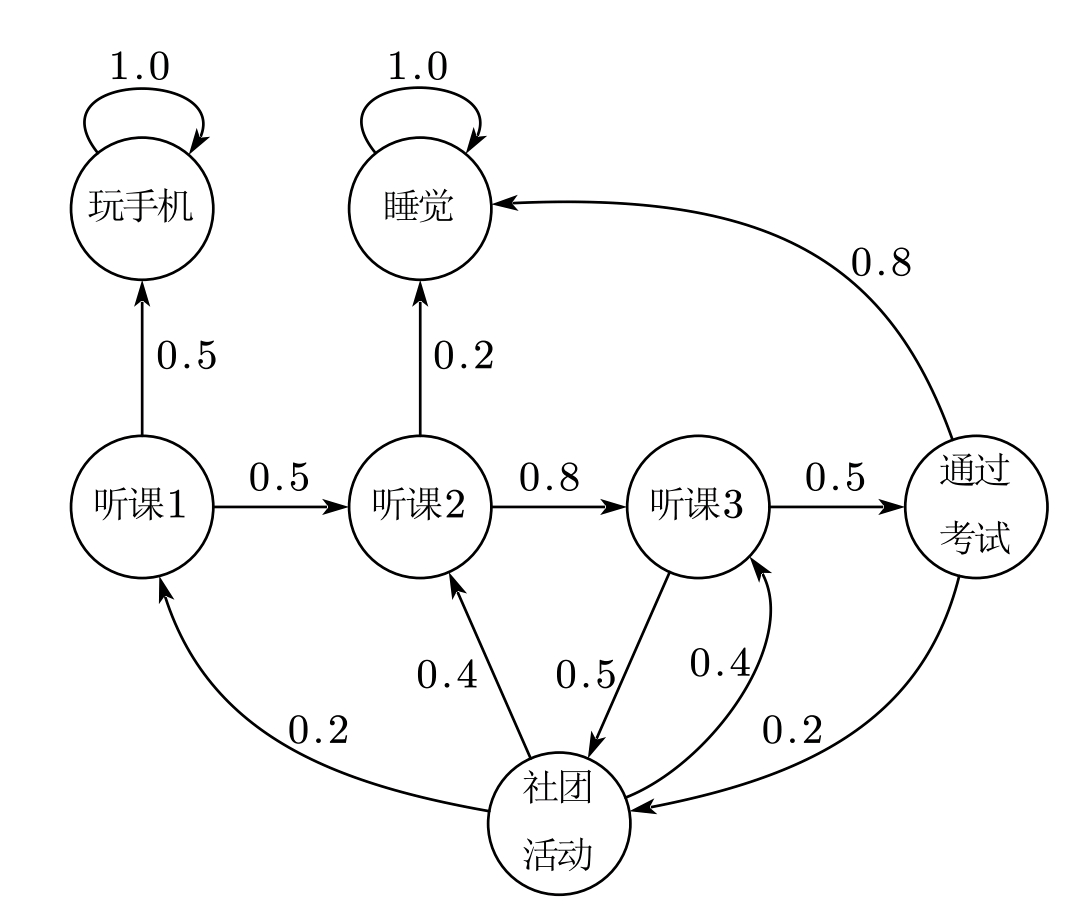
(1)试写出一步转移概率矩阵$P(1)$,并指出其中哪一状态为吸收态,哪一种状态为常返态,哪一种状态为非常返态
(2)试写出$n$趋于无穷时的转移概率矩阵$\lim\limits_{n \to + \infty}P(n)$,并适当说明求解过程(不要求严格证明)
五、某赌徒参加一场游戏,身上有初始资金$a, 0 < a < m, a \in Z^+$,假设他每局以相同概率$p$赢一元,同时以概率$1-p$输掉一元。假设不同的赌局之间的结果是互相独立的。当赌徒资金达到总数$m$或输掉全部资金时游戏结束,请问游戏结束时资金到达$m$或者输掉全部资金的概率是多少?(需必要文字和状态转移图说明,不要求严格证明)
参考答案
一. 证明略(提示:甲乙两人在第$n+1$次交换后拥有球的数目仅与第$n$次交换后的数目有关,而与第$n$次前无关),状态转移图略,转移矩阵如下:
$$P(1)=\begin{bmatrix} 0&1&0&0\\ 1/9&4/9&4/9&0\\ 0&4/9&4/9&1/9\\ 0&0&1&0 \end{bmatrix}$$
二.仅给出$P^2=P(2)$的简要证明,$P^n=P(n)$可用数学归纳法证明
参考例三和全概率公式,根据题意有
$$p_{00}(2)=p_{00}\times p_{00}+p_{01}\times p_{10}$$
$$p_{10}(2)=p_{10}\times p_{00}+p_{11}\times p_{10}$$
$$p_{01}(2)=p_{00}\times p_{01}+p_{01}\times p_{11}$$
$$p_{11}(2)=p_{10}\times p_{01}+p_{11}\times p_{11}$$
故
$$P(2)=\begin{bmatrix}
p_{00}\times p_{00}+p_{01}\times p_{10}&p_{00}\times p_{01}+p_{01}\times p_{11}\\
p_{10}\times p_{00}+p_{11}\times p_{10}&p_{10}\times p_{01}+p_{11}\times p_{11}
\end{bmatrix}$$
根据题中所给矩阵乘法定义有:
$$P^2=\begin{bmatrix}
p_{00}\times p_{00}+p_{01}\times p_{10}&p_{00}\times p_{01}+p_{01}\times p_{11}\\
p_{10}\times p_{00}+p_{11}\times p_{10}&p_{10}\times p_{01}+p_{11}\times p_{11}
\end{bmatrix}=P(2)$$
三.根据题意有$p_{00}=p_{01}=p_{10}=p_{11}=1/2$
根据定义7和定义8有
$f_{00}=\sum\limits_{n=1}^{\infty}f_{00}(n)=p_{10}+p_{11}\times p_{10}+p_{11}^2\times p_{10}+p_{11}^3\times p_{10}+ \cdots p_{11}^n\times p_{10}+\cdots= \sum\limits_{n=1}^{\infty}{\dfrac{1}{2^n}} =1$
满足常返态定义,状态1同理可证
四.(1)分别定义玩手机,听课程1,听课程2, 听课程3, 通过考试,去社团活动,睡觉这七种状态分别为$0, 1, 2, 3, 4, 5, 6$,一步状态转移矩阵$P$有
$$P(1)=\begin{bmatrix}
1&0&0&0&0&0&0\\
1/2&0&1/2&0&0&0&0\\
0&0&0&4/5&0&0&1/5\\
0&0&0&0&1/2&1/2&0\\
0&0&0&0&0&1/4&4/5\\
0&1/2&2/5&2/5&0&0&0\\
0&0&0&0&0&0&1
\end{bmatrix}$$
其中状态0和6均为常返态和吸收态,其他均为非常返态
(2)设这七种状态最终到达另一种状态的概率为$a_{ij}(i,j=0,1,2,3,4,5,6)$。考虑命题1和定义6有$a_{00}=a_{66}=1, a_{mn}=0(m=1,2,3,4,5, n \neq 0, 6)$
考虑如下等式
$$a_{10}=0.5a_{00}+0.5a_{20} (1)$$
$$a_{20}=0.8a_{30}+0.2a_{60} (2)$$
$$a_{30}=0.5a_{40}+0.5a_{50} (3)$$
$$a_{40}=0.8a_{40}+0.2a_{50} (4)$$
$$a_{50}=0.2a_{10}+0.4a_{20}+0.4a_{30} (5)$$
又$a_{00}=a_{66}=1$,解得$a_{10}=71/130, a_{20}=6/65, a_{30}=3/26, a_{40}=1/26, a_{50}=5/26$
又有$a_{i6}=1-a_{i0}, (i \neq 0,6)$, 则$a_{60}=59/130, a_{26}=59/65, a_{36}=23/26, a_{46}=25/26, a_{56}=21/26$(实际上,也可通过上述同样方法求出,不过运算较麻烦)
则$$P(\infty)=\begin{bmatrix}
1&0&0&0&0&0&0\\
71/130&0&0&0&0&0&59/130\\
6/65&0&0&0&0&0&59/65\\
3/26&0&0&0&0&0&23/26\\
1/26&0&0&0&0&0&25/26\\
5/26&0&0&0&0&0&21/26\\
0&0&0&0&0&0&1
\end{bmatrix}$$
另给出上述方法的简要证明:假设$A$表示某常返态状态$s$最终被到达的事件,$i$为状态空间中某一非常返态,则有
$$a_{is}=P(A | X_{0}=i )=\sum_{j=0}^{m}P(A | X_{0}=i, X_{1}=j)P(X_{1}=j | X_{0}=i)=\sum_{j=0}^{m}P(A | X_{1}=j)p_{ij}$$
$$a_{is}=\sum_{j=0}^{m}a_{js}p_{ij}$$
举例, 由命题1和上式有对于等式(1)就有$$a_{10}=0.5a_{00}+0.5a_{20}+0(a_{30}+a_{10}+a_{40}+a_{50}+a_{60})$$
五.我们建立马尔可夫链模型,状态i表示每次赌局开始时赌徒的资金,状态$i=0$和$i=m$分别表示输和赢.
除了输和赢的状态是吸收的,其余状态均为非常返态.
设$\rho_{i,m}$,$\rho_{i,0}$分别为状态i最终到达状态m,状态0的概率.当$2 \leq i \leq m-2$时有
$$\rho_{i,m}=p\rho_{i+1,m}+(1-p)\rho_{i-1,m} \qquad (1)$$
还有
$$\rho_{m-1,m}=(1-p)\rho_{m-2,m}+p \qquad (2)$$
以及
$$\rho_{1,m}=p\rho_{2,m}+(1-p)\rho_{0,m}=p\rho_{2,m} \qquad (3)$$
根据(1)有
$$(1-p)(\rho_{i,m}-\rho_{i-1,m})=p(\rho_{i+1,m}-\rho_{i,m}),\quad (i=1,\cdots ,m-1)$$
令$\theta$=$\dfrac{1-p}{p}$,联立(2),(3)有
$$\rho_{i,m}=
\begin{cases}
\dfrac{1-\theta^i}{1-\theta^m} &\theta\ne 1\\
\dfrac{i}{m} &\theta=1
\end{cases}$$
故当$p=\dfrac{1}{2}$时,最终赢的概率为$\dfrac{a}{m}$,
$p\ne\dfrac{1}{2}$时,最终赢的概率为$\dfrac{1-\theta^a}{1-\theta^m}$.
