未来技术学院 2021 年选拔考试(数学)参考答案
答案说明
- 未来技术学院未公开发布试卷内容,回忆版试卷内容请浏览往届老生整理的词条:未来技术学院 2021 年选拔考试(数学) ;
- 未来技术学院未公开发布试卷标准答案,本词条内容为往届老生整理的参考答案,无法保证答案的完全准确性与最优性,仅供学习参考;
- 欢迎指出本套答案的不足点,或提供更好的解题思路;
参考答案
1.
解:
∵ $i = \cos \dfrac{π}{2} + i\sin \dfrac{π}{2} = e^{\tfrac{π}{2}}$
∴ $i^n = e^{\tfrac{πn}{2}i} = \cos \dfrac{πn}{2} + i\sin \dfrac{πn}{2}$
∵ $1 + \sqrt 3 i = 2(\dfrac {1}{2} + \dfrac {\sqrt3}{2}i)$
$= 2(\cos \dfrac{π}{3} + i\sin \dfrac{π}{3}) = 2e^{\tfrac{π}{3}i}$
∴$(1 + \sqrt 3 i)^n = 2^ne^{\tfrac{πn}{3}i}$
$= 2^n(\cos \dfrac{πn}{3} + i\sin \dfrac{πn}{3})$
2.
证明:
设 $z_1 = a_1 + b_1i$ , $z_2 = a_2 + b_2i$
∴ $LHS = (a_1 + a_2)^2 + (b_1 + b_2)^2 $
$= (a_1^2 + b_1^2) + (a_2^2 + b_2^2) + 2(a_1a_2 + b_1b_2)$ = RHS
∵ $-|z_1||z_2|\cos t \leq -|z_1||z_2| \leq -|z_1z_2|$
$\leq Re(z_1\overline z_2) \leq $ $|z_1z_2| \leq |z_1||z_2| \leq |z_1||z_2|\cos t$
∴ $|z_1| - |z_2| \leq |z_1+z_2| $
$= \sqrt{|z_1|^2+|z_2|^2+2Re(z_1\overline{z_2})} \leq |z_1| + |z_2|$
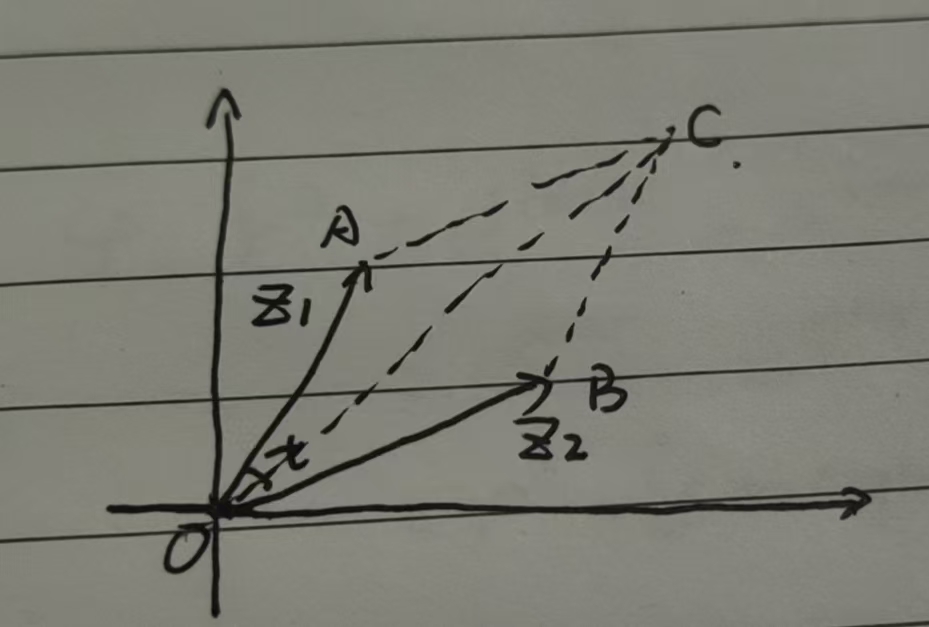
如下图所示,$|z_1| = ||\mathbf{OA}||$ , $|z_2| = ||\mathbf{OB}||$ , $|z_1 + z_2| = ||\mathbf{OC}||$,
即三角形两边之和大于第三边,两边之差小于第三边。
图片:问题 2 示意图
(图片来源:彭宇阳)
3.
解:
设 $z_1 = x_1 + y_1i$ , $z_2 = x_2 + y_2i$ , $z = x + yi$
∵ $|\dfrac{z-z_1}{z-z_2}| = \dfrac{|z-z_1|}{|z-z_2|}< 1 $
∴ $|z-z_1|<|z-z_2|$
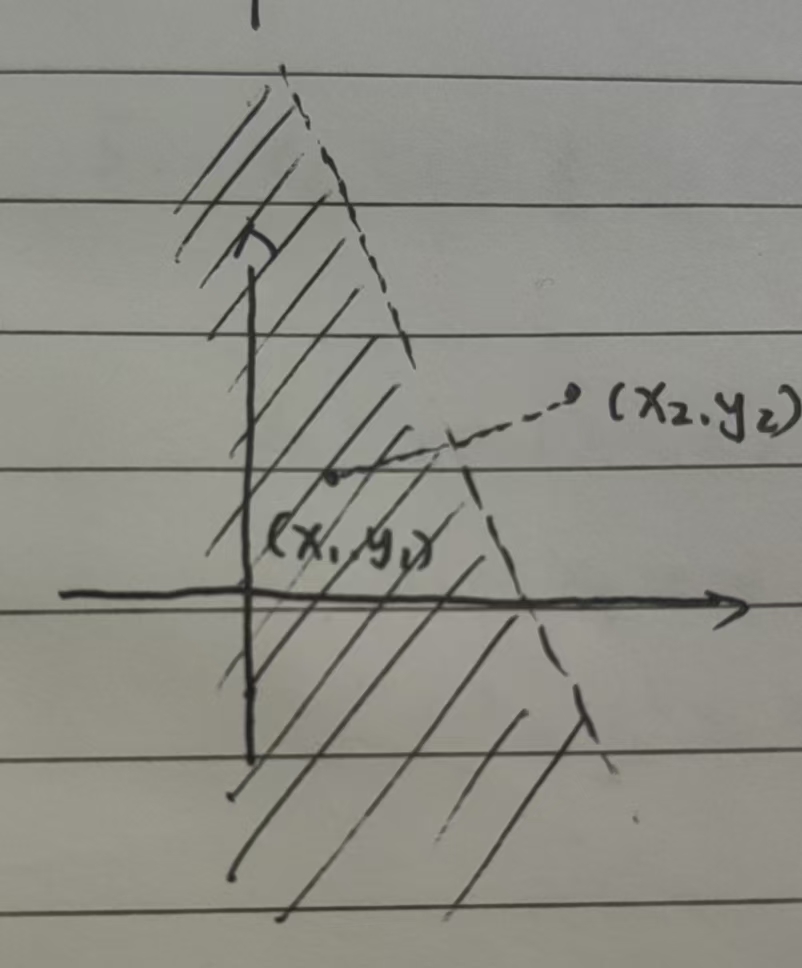
由于两复数之差的模表示复平面上两点之间的距离,故上式表示$(x,y)$与$(x_1,y_1)$之间的距离小于$(x,y)$与$(x_2,y_2)$之间的距离,绘制 E 的图像如下图所示:
图片:问题 3 示意图
(图片来源:彭宇阳)
4.
解:
$r^z = e^{zlnr} = e^{xlnr +iylnr}$
$= r^x(\cos(ylnr) + i\sin(ylnr))$
5.
证明:
① 当$z_1$、$z_2$、$z_3$为正三角形的三个顶点时,不妨假设$z_1 = e^{i\theta},z_2 = e^{i(\theta+\tfrac{2π}{3})},z_3 = e^{i(\theta+\tfrac{4π}{3})}$
则有
$z_1 + z_2 + z_3 = e^{i\theta}(1 + e^{\tfrac{2π}{3}i} + e^{\tfrac{4π}{3}i}) = 0$
得证
② 当$z_1+z_2+z_3=0$时,不妨假设$z_1 = e^{i\theta},z_2 = e^{i(\theta+\theta_1)},z_3 = e^{i(\theta+\theta_2)}$,其中$\theta_1 \neq \theta_2$
则有
$z_1 + z_2 + z_3 = e^{i\theta}(1 + e^{\theta_1i} + e^{\theta_2i}) = 0$
∴ $\cos \theta_1 + \cos \theta_2 + 1 = 0$
且 $\sin \theta_1 + \sin \theta_2 = 0$
解得:$\theta_1 = \dfrac{2π}{3}$,$\theta_2 = \dfrac{4π}{3}$ 或 $\theta_1 = \dfrac{4π}{3}$,$\theta_2 = \dfrac{2π}{3}$
故$z_1$、$z_2$、$z_3$为正三角形的三个顶点。
