未来技术学院 2023 年选拔考试(数学)参考答案
答案说明
- 未来技术学院未公开发布试卷内容,回忆版试卷内容请浏览往届老生整理的词条:未来技术学院 2023 年选拔考试(数学) ;
- 未来技术学院未公开发布试卷标准答案,本词条内容为往届老生整理的参考答案,无法保证答案的完全准确性与最优性,仅供学习参考;
- 欢迎指出本套答案的不足点,或提供更好的解题思路;
参考答案
一.
1.
证明:
$S_{\triangle OUV} = \dfrac{1}{2}||\mathbf{U}||||\mathbf{V}||\sin(t) $
$= \dfrac{1}{2}\sqrt{(||\mathbf{U}||||\mathbf{V}||\sin(t))^2} $
$= \dfrac{1}{2}\sqrt{(||\mathbf{U}||||\mathbf{V}||)^2(1 - (\cos(t))^2)} $
$= \dfrac{1}{2}\sqrt{(||\mathbf{U}||||\mathbf{V}||)^2 - (\mathbf{U}\mathbf{V})^2} $
图片:问题 1 示意图
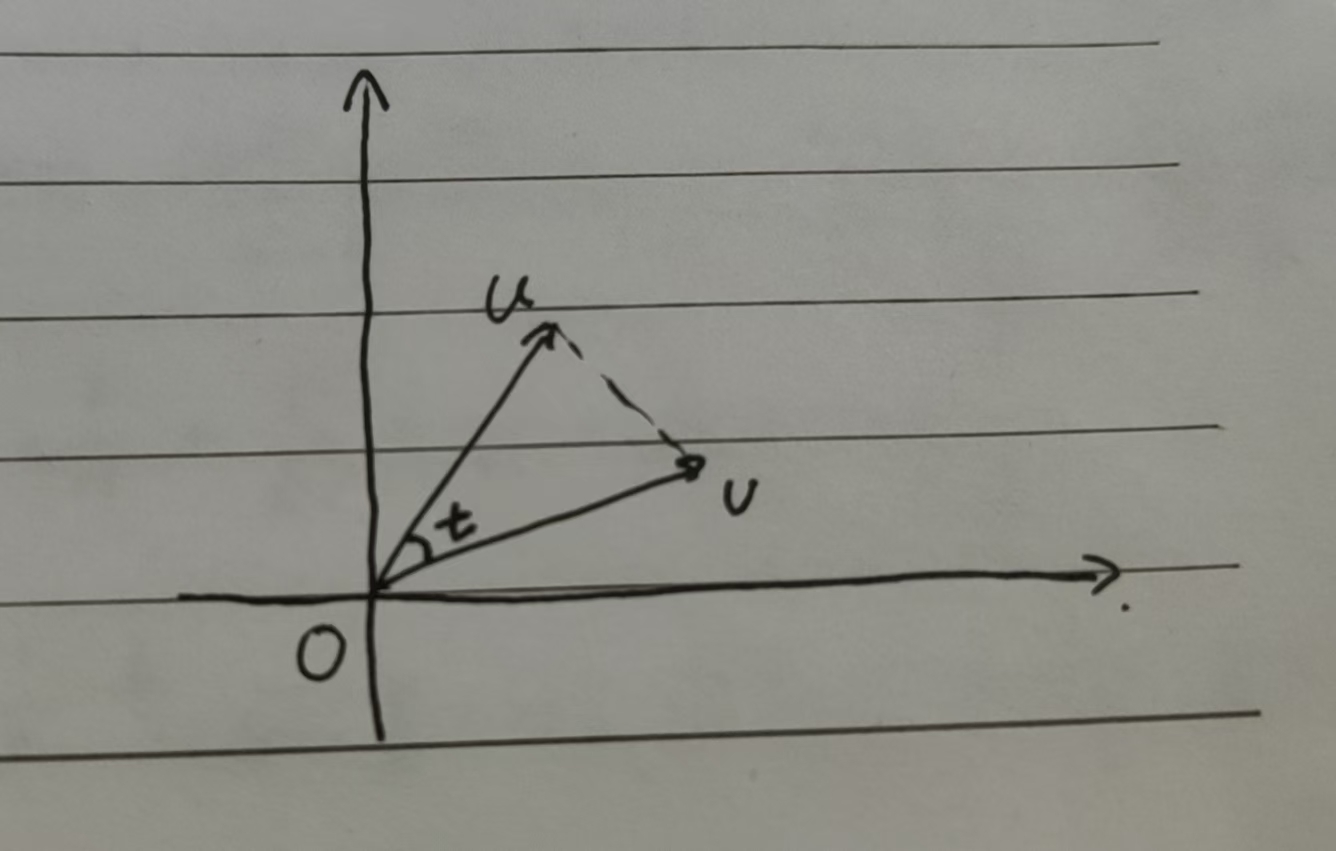
(图片来源:彭宇阳)
2.
证明:
$S_{\triangle OUV} = \dfrac{1}{2}\sqrt{(||\mathbf{U}||||\mathbf{V}||)^2 - (\mathbf{U}\mathbf{V})^2} $
$= \dfrac{1}{2}\sqrt{(u_1^2 + u_2^2)(v_1^2 + v_2^2)-(u_1v_1 + u_2v_2)^2}$
$= \dfrac{1}{2}\sqrt{(u_1v_2 - u_2v_1)^2} $
$= \dfrac{1}{2}|u_1v_2 - u_2v_1|$
二.
1.
证明:
采用数学归纳法:
① n = 2 时:
LHS = $\displaystyle\sum^2_{k=1}a_kb_k$ = $a_1b_1 + a_2b_2$ = RHS
② n ≥ 3 时:
LHS = $\displaystyle\sum^{n-1}_{k=1}a_kb_k + a_nb_n$
= $S_{n-1}b_{n-1} + \displaystyle\sum^{n-2}_{k=1}S_k(b_k-b_{k+1}) + a_nb_n$
=$ S_{n-1}b_{n-1} + \displaystyle\sum^{n-1}_{k=1}S_k(b_k-b_{k+1}) - S_{n-1}(b_{n-1}-b_n) + a_nb_n$
= $(S_{n-1}b_n + a_nb_n) + \displaystyle\sum^{n-1}_{k=1}S_k(b_k-b_{k+1})$
=$ S_nb_n+\displaystyle\sum^{n-1}_{k=1}S_k(b_k-b_{k+1})$
2.
证明:
设 $a_k = \cos(kx)$ ,$ b_k = \dfrac{1}{k} $
由欧拉公式可得:
$\displaystyle\sum^{n}_{k=1}\cos(kx) + i\displaystyle\sum^{n}_{k=1}\sin(kx)$
= $\displaystyle\sum^{n}_{k=1}(\cos(kx) + i\sin(kx))$
= $\displaystyle\sum^{n}_{k=1}e^{ikx}$
= $\dfrac{(e^{inx} - 1)e^{ix}}{e^{ix} - 1}$
= $\dfrac{2ie^{\tfrac{inx}{2}}e^{ix}\sin(\dfrac{nx}{2})}{2ie^{\tfrac{ix}{2}}\sin(\dfrac{x}{2})}$
= $\dfrac{\sin(\dfrac{nx}{2})}{\sin(\dfrac{x}{2})}e^{\tfrac{i(n+1)x}{2}}$
= $\dfrac{\sin(\dfrac{nx}{2})}{\sin(\dfrac{x}{2})}(\cos(\dfrac{(n+1)x}{2}) + i\sin(\dfrac{(n+1)x}{2}))$
∴ $S_k = a_1 + a_2 +\cdots + a_k = \dfrac{\sin(\dfrac{kx}{2})\cos(\dfrac{(k+1)x}{2})}{\sin(\dfrac{x}{2})}$
∴ LHS = $\displaystyle\sum^n_{k=1}\dfrac{\cos({kx})}{k}$
= $\dfrac{\sin(\dfrac{nx}{2})\cos(\dfrac{(n+1)x}{2})}{n\sin(\dfrac{x}{2})} + \displaystyle\sum^{n-1}_{k=1}(\dfrac{1}{n} -\dfrac{1}{n+1})\dfrac{\sin(\dfrac{kx}{2})\cos(\dfrac{(k+1)x}{2})}{\sin(\dfrac{x}{2})}$
≤ $\dfrac{1}{n\sin(\dfrac{x}{2})} + \displaystyle\sum^{n-1}_{k=1}(\dfrac{1}{k} -\dfrac{1}{k+1})\dfrac{1}{\sin(\dfrac{x}{2})} = \dfrac{1}{\sin(\dfrac{x}{2})}$
3.
证明:
$\displaystyle\sum^N_{k=1}a_kb_k = S_Nb_N - \displaystyle\sum^{N-1}_{k=1}S^{(1)}_k \Delta ^{(1)} b_k$
由于 $k>N$ 时,$b_k=0$
∴ 原式 = $(S_Nb_N - S_Nb_{N+1}) - \displaystyle\sum^{N-1}_{k=1}S^{(1)}_k \Delta ^{(1)} b_k$
= $-\displaystyle\sum^N_{k=1}S^{(1)}_k \Delta ^{(1)} b_k$
= $-((\displaystyle\sum^N_{k=1}S^{(1)}_k)\Delta ^{(1)} b_k + \displaystyle\sum^{N-1}_{k=1}(\displaystyle\sum^N_{k=1}S^{(1)}_k)(\Delta ^{(1)} b_k - \Delta ^{(1)} b_{k+1}))$
= $-S^{(2)}_k\Delta ^{(1)} b_k + \displaystyle\sum^{N-1}_{k=1}S^{(2)}_k \Delta ^{(2)} b_k $
= $(-1)^2\displaystyle\sum^N_{k=1}S^{(2)}_k \Delta ^{(2)} b_k$
以此类推可得证。
三.
答:
两周期函数之和不一定为周期函数。考虑以下反例(答案不唯一):
$f_1(x) = \sin x$ , $f_2(x) = \sin(\alpha x)$, 其中 $\alpha$ 为无理数
$g(x) = f_1(x) + f_2(x) = \sin x + \sin(\alpha x)$
若 $g(x)$ 周期为 $T$,则有 $ g(x) = g(x+T)$,即
$ \sin x + \sin(\alpha x) = \sin(x+T) + \sin(\alpha(x+T))$
LHS = $-2\cos(\alpha x+\dfrac{\alpha T}{2})\sin(\dfrac{\alpha T}{2}) = 2\cos(x+\dfrac{T}{2})\sin(\dfrac{T}{2})$ = RHS
取 $x = \dfrac{π}{2} - \dfrac{T}{2}$,则 $\sin(\dfrac{\alpha T}{2}) = 0$
故 $\alpha T = 2pπ$
取 $\alpha x = \dfrac{π}{2} - \dfrac{\alpha T}{2}$,则 $\sin(\dfrac{T}{2}) = 0$
故 $T = 2qπ$,其中 $p$、$q$ 为非零整数
故 $ \alpha T = 2pπ = 2\alpha qπ$,即 $\alpha = \dfrac{p}{q}$,这与$\alpha$为无理数相矛盾。
