未来技术学院 2022 年选拔考试(数学)参考答案
答案说明
- 未来技术学院未公开发布试卷内容,回忆版试卷内容请浏览往届老生整理的词条:未来技术学院 2022 年选拔考试(数学) ;
- 未来技术学院未公开发布试卷标准答案,本词条内容为往届老生整理的参考答案,无法保证答案的完全准确性与最优性,仅供学习参考;
- 欢迎指出本套答案的不足点,或提供更好的解题思路;
参考答案
一.
1.
证明:
设$\mathbf{U} = (x_1,y_1)$,$\mathbf{V} = (x_2,y_2)$
$LHS = (x_1-x_2)^2 + (y_1-y_2)^2$
$= (x_1^2+y_1^2) + (x_2^2 + y_2^2) - 2(x_1x_2 + y_1y_2)$
$= RHS$
图片:问题 1 示意图
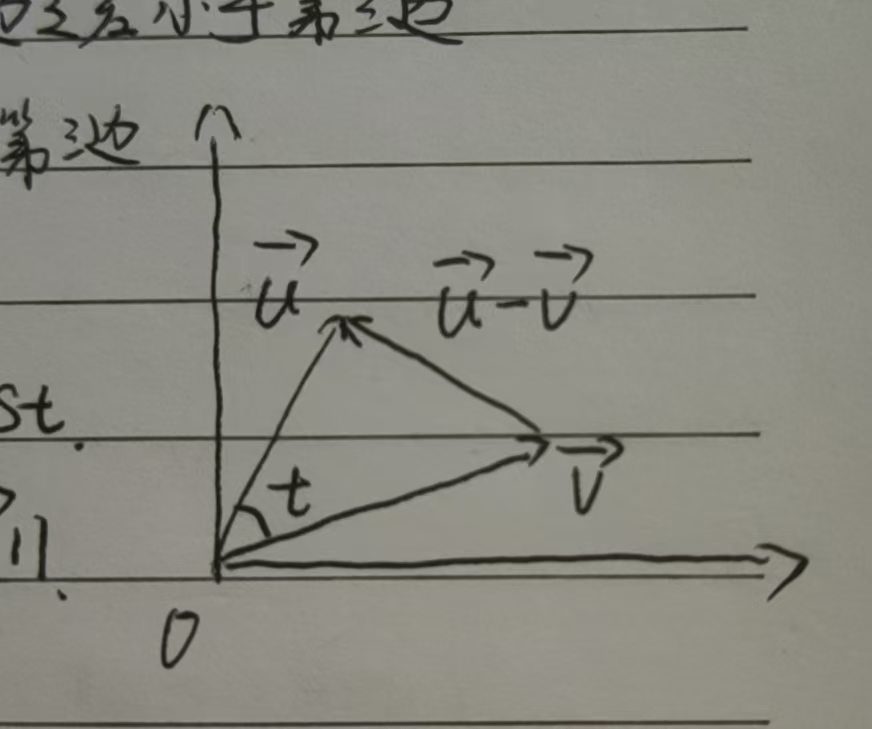
(图片来源:彭宇阳)
由图可知$||\mathbf{U}-\mathbf{V}||$可以表示三角形第三条边的长度,又由不等式:
$||\mathbf{U}||-||\mathbf{V}|| \leq ||\mathbf{U} - \mathbf{V}||$ $= \sqrt{||\mathbf{U}||^2+||\mathbf{V}||^2-2\mathbf{U}\mathbf{V}} \leq ||\mathbf{U}||+||\mathbf{V}||$
可知,三角形两边之和大于第三边,两边之差小于第三边。
2.
证明:
由余弦定理可知:
$||\mathbf{U}-\mathbf{V}||^2=||\mathbf{U}||^2+||\mathbf{V}||^2-2||\mathbf{U}||||\mathbf{V}||\cos t$
∴$\mathbf{U}\mathbf{V} = ||\mathbf{U}||||\mathbf{V}||\cos t \leq ||\mathbf{U}||||\mathbf{V}||$
二.
1.
证明:
由于向量$\mathbf{U}$的端点 U 到原点 O 的距离始终保持不变,故原向量$\mathbf{U}$与坐标系变动之后的向量$\mathbf{U'}$范数相同,故:
$||\mathbf{U}||^2 = x^2 +y^2 = ||\mathbf{U'}||^2 = x'^2 +y'^2$
2.
证明:
如图所示:
图片:问题 2 示意图
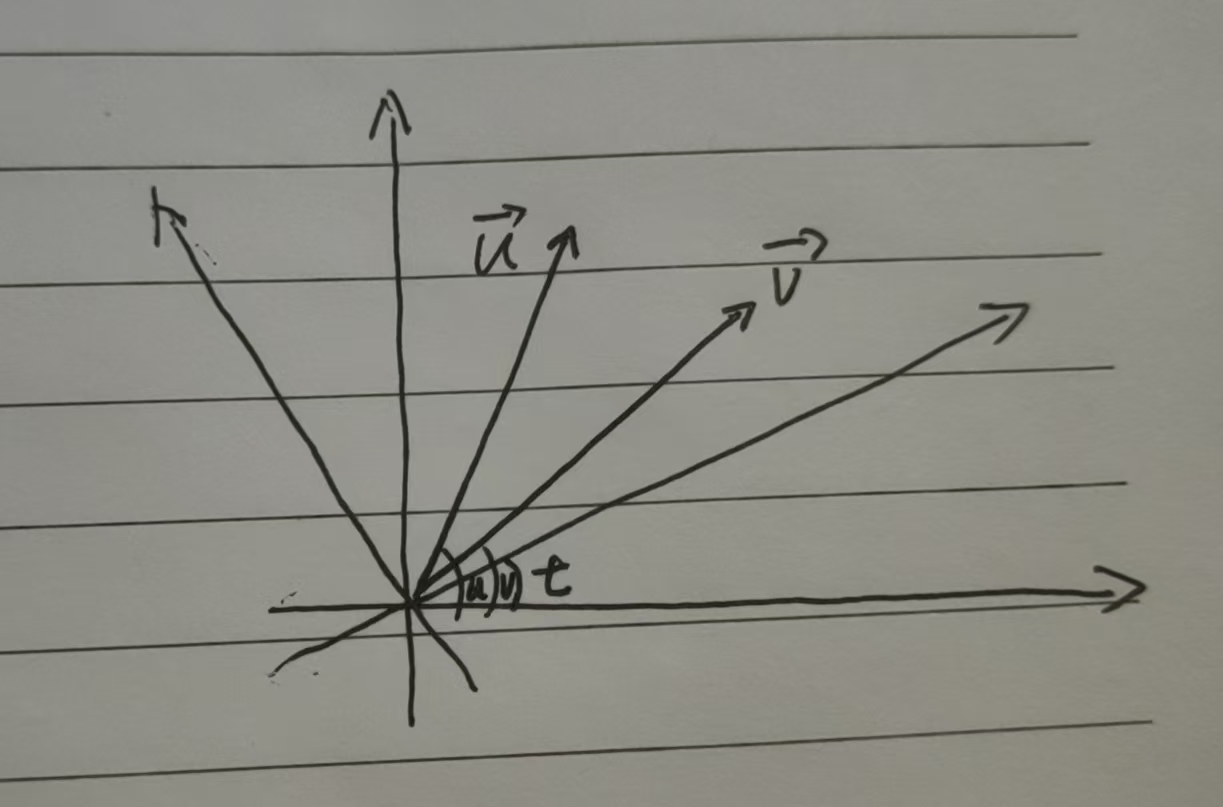
(图片来源:彭宇阳)
设$u_1 = ||\mathbf{U}||\cos u$,$u_2 = ||\mathbf{U}||\sin u$,
$v_1 = ||\mathbf{V}||\cos v$,$v_2 = ||\mathbf{V}||\sin v$,
$u'_1 = ||\mathbf{U}||\cos(u-t)$,$u'_2 = ||\mathbf{U}||\sin(u-t)$,
$v'_1 = ||\mathbf{V}||\cos(v-t)$,$v'_2 = ||\mathbf{V}||\sin(v-t)$
∴ $LHS = ||\mathbf{U}||||\mathbf{V}||(\cos u \cos v + \sin u \sin v)$
$= ||\mathbf{U}||||\mathbf{V}||\cos(u-v)$
$= ||\mathbf{U}||||\mathbf{V}||\cos((u-t)-(v-t))$
$= ||\mathbf{U}||||\mathbf{V}||(\cos(u-t) \cos(v-t) + \sin(u-t) \sin(v-t))$
$= RHS$
3.
证明:
将第二问中的$t$替换为$\theta$即得证。
