未来技术学院 2022 级选拔考试（数学）
答题时间：90分钟（含阅读材料时间）
说明：
1.本考试为材料阅读分析，根据材料现场作答
2.本试题为考场回忆，与实际试题可能存在部分偏差，未来技术学院并未公开试卷。
3.数学选拔考试旨在选拔具有数学逻辑分析，推导，缜密论证能力的同学，因此阅读材料很可能是从任何一个大学课程或者其他教材中摘取的部分，本试题仅供参考考试形式，答案自行搜集
关于二维空间与三维空间向量，我们在过去接触过．那么为了便于大家理解，我们这里仅以二维向量为背景．所以，我们介绍二维向量的概念，运算以及简单性质．供大家解决后面问题时参考．
定义1．一个有序实数数组称为一个二维向量，我们用大写英文字母表示 $$\mathbf{U}=(u_1,u_2).$$ 数$u_1$和$u_2$称为向量$\mathbf{U}$的分量．二维向量的全体称为二维向量空间,记为$\mathbf{R^2}$．
运算 对二维向量，我们引入以下代数运算：
(1)设$c$为实数， $$c\mathbf{U}=(cu_1,cu_2).$$
(2)设向量$\mathbf{U}=(u_1,u_2)$与$\mathbf{V}=(v_1,v_2)$，
$$\mathbf{U}+\mathbf{V}=(u_1+v_1,u_2+v_2).$$
注记 记$(0,0)$为$\mathbf{O}$，并称之为零向量．注意，对每个向量$\mathbf{U}$，都有$\mathbf{U}+\mathbf{O}=\mathbf{U}$．记$(-u_1,-u_2)=-\mathbf{U}$．向量$\mathbf{V}-\mathbf{U}$定义为$\mathbf{V}+(-\mathbf{U})$，称为$\mathbf{V}$与$\mathbf{U}$的差．
向量$\mathbf{U}=(x,y)$可以用平面里面的点来描述，我们把$(x,y)$称为向量$\mathbf{U}$的坐标．
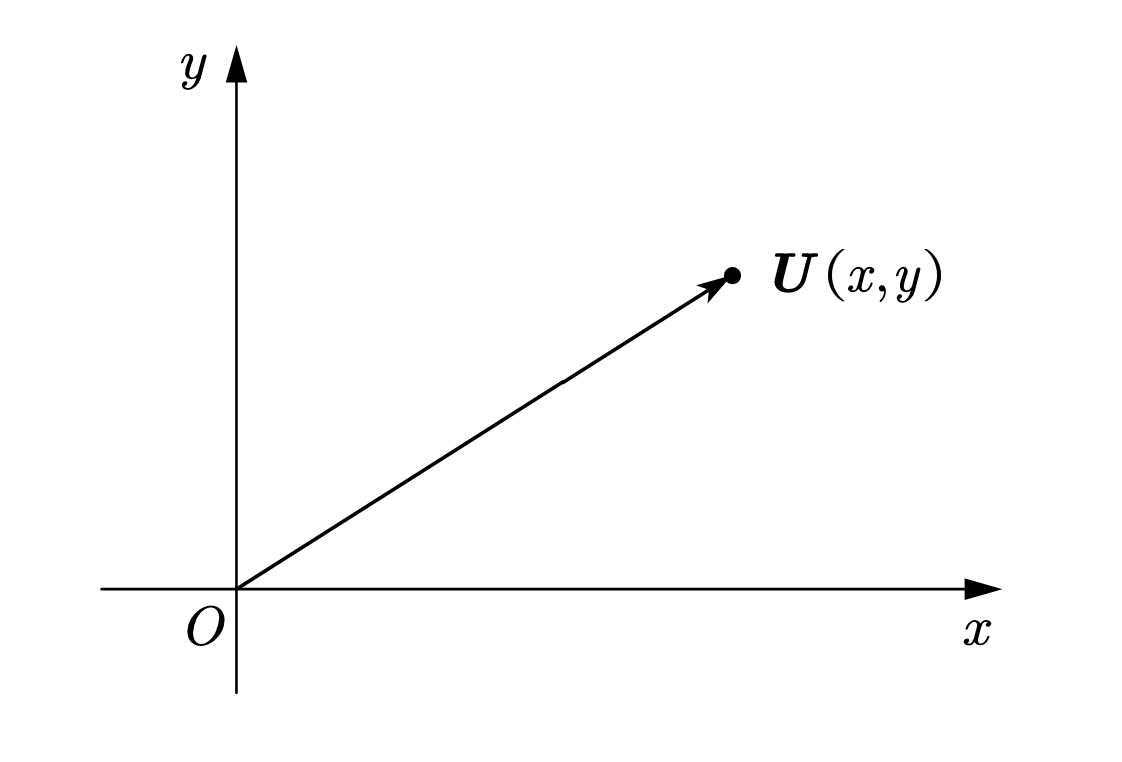
定义2．向$\mathbf{U}$与$\mathbf{V}$的一个线性组合定义为 $$a\mathbf{U}+b\mathbf{V},$$ 其中$a$和$b$为实数．
定义3．从$\mathbf{R^2}$到实数集的一个函数$f:$ $\mathbf{U}$→$f(\mathbf{U})$如果满足下面的性质，就称为线性函数．对于任意的实数$c$和向量$\mathbf{U}$，$\mathbf{V}$，满足
(1) $$f(c\mathbf{U})=cf(\mathbf{U}),$$
(2) $$ f(\mathbf{U}+\mathbf{V})=f(\mathbf{U})+f\mathbf{V}). $$
定义4．设向量$\mathbf{U}=(x,y)$，定义 $$ ||\mathbf{U}||=\sqrt{x^2+y^2} $$ 为向量$\mathbf{U}$的范数，称$||\mathbf{U}||=1$的向量$\mathbf{U}$为单位向量．
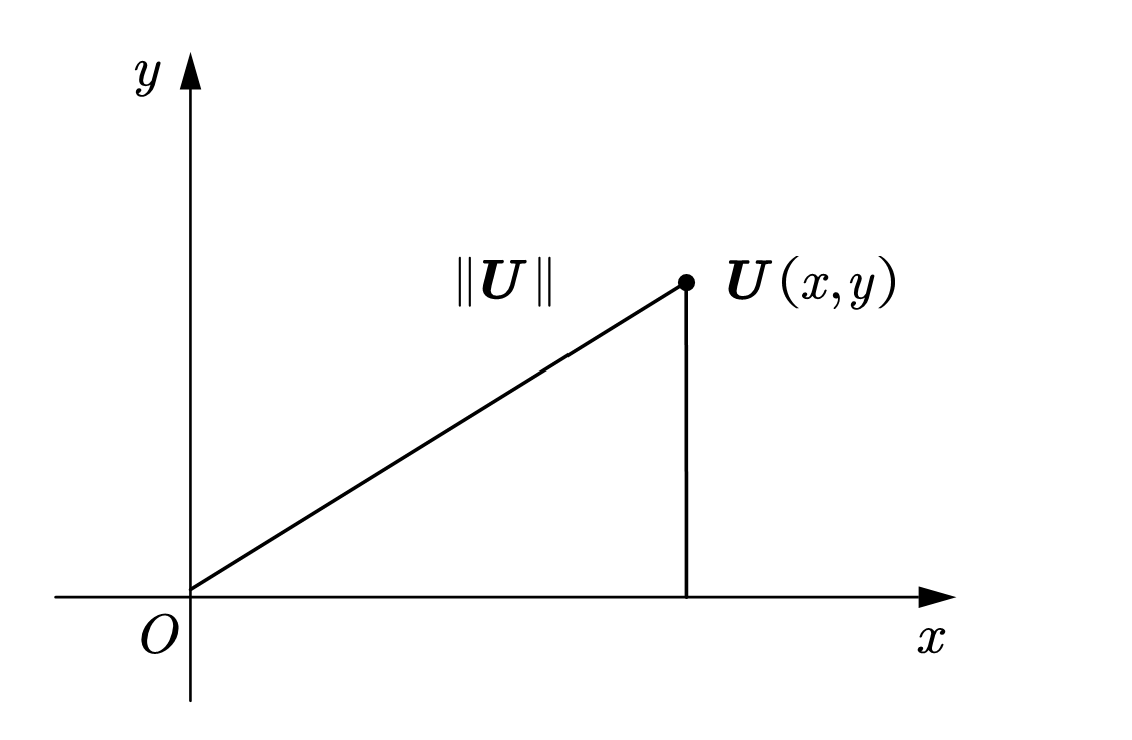
从图中可以看出，向量$\mathbf{U}=(x,y)$的范数$||\mathbf{U}||$为点$(x,y)$到原点$(0,0)$的距离．
与向量范数密切相关的一个概念，是两个向$\mathbf{U}$和$\mathbf{V}$的数量积（点积）．
定义5．设向量$\mathbf{U}=(u_1,u_2)$和$\mathbf{V}=(v_1,v_2)$，$U$和$V$的内积定义为 $$ \mathbf{UV}=u_1v_1+u_2v_2. $$
向量的数量积与两个数的乘法有类似的性质， (1)分配律：对向量$\mathbf{U}$，$\mathbf{V}$，$\mathbf{W}$有 $$ \mathbf{U(V+W)}=\mathbf{UV}+\mathbf{UW}; $$ (2)交换律：对向量$\mathbf{U}$，$\mathbf{V}$有 $$ \mathbf{UV}=\mathbf{VU}. $$
性质 利用上述定义，可以得到： $$ \mathbf{UU}=||\mathbf{U}||^2. $$
问题
一、设$\mathbf{U}$与$\mathbf{V}$为二维向量.
(1)证明下述等式，并解释等式的几何含义． $$ ||\mathbf{U}-\mathbf{V}||^2=||\mathbf{U}||^2+||\mathbf{V}||^2-2\mathbf{U}\mathbf{V}. $$ (2)由(1)，容易得到不等式：$\mathbf{UV} \leq \frac{1}{2} ||\mathbf{U}||^2+\frac{1}{2} ||\mathbf{V}||^2$，利用(1)，证明下面更强的不等式： $$ \mathbf{UV} \leq ||\mathbf{U}||\,||\mathbf{V}||. $$
二、如图，设坐标轴$x$，$y$被经过原点的另外一对垂直的直线代替，$(x',y')$是向量$\mathbf{U}=(x,y)$在新坐标系下的坐标．
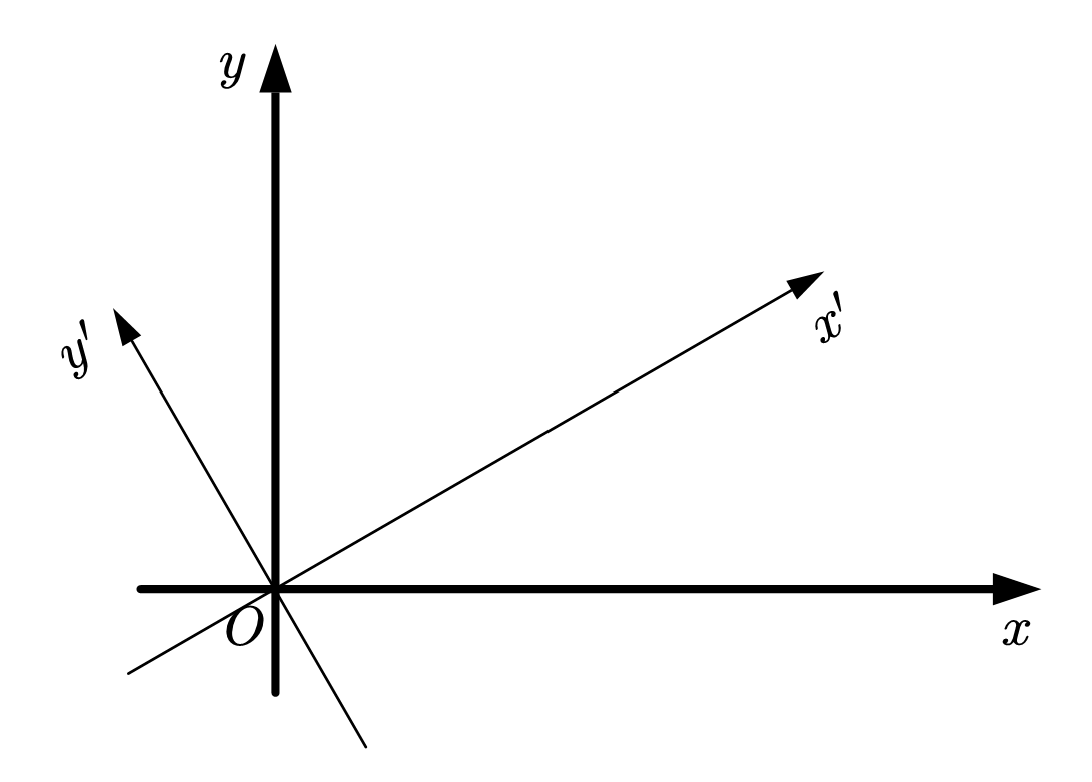
(1)证明 $$ x'^2+y'^2=x^2+y^2. $$
(2)设向量$\mathbf{U}=(u_1,u_2)$与$\mathbf{V}=(v_1,v_2)$在新坐标系下的坐标分别为$(u_1',u_2')$与$(v_1',v_2')$．证明： $$ u_1v_1+u_2v_2=u_1'v_1'+u_2'v_2'. $$ (3)利用(2)证明 $$ \mathbf{UV}=||\mathbf{U}||\,||\mathbf{V}||\,\cos\theta, $$ 其中$\theta$为$\mathbf{U}$与$\mathbf{V}$的夹角．