未来技术学院 2023 级选拔模拟考试(数学)样题
考前须知
- 根据阅读材料,完成后面的 4 道题,每道题建议用时 1 ~ 2 个小时;
- 本试题由往届学长根据 2018 级、2019 级、2020 级求是数学选拔考试试题,以及 2020 级、2021 级、2022 级未来技术学院(原求是学部)选拔考试(数学部分)的考场回忆编写的样题。并随机摘选大学课程内容编写而成。本题只具有题目形式的参考意义。既不代表最终难度,也不代表实际考试内容,更不代表求是学部,和数学学院。还请谨慎看待这张试题难度、题型以及内容;
- 本试题为大学课程内容随机摘选,若有纰漏请与笔者联系,望周知;
- 试题适用范围:未来技术学院,求是数学班(数学拔尖计划)选拔考试;
不适用范围:化工学院领军计划、王守融班、吴咏诗班及其他拔尖计划
阅读材料
Part I
离散时间序列为数字信号处理中常用的数学表示,其通常指一组序列$ f(n) $,其中$ n $为时间,$ n=0 $时表示时刻$ 0 $,$ n=1 $时表示时刻$ 1 $,依此类推。通常一组离散时间序列也可以称之为 数字信号,这里$ n\in Z $。
对于序列$ f(n) $在$ n $时刻的取值,我们定义为信号$ f $在$ n $时刻的 信号强度。下面我们来看两种常见基本信号:
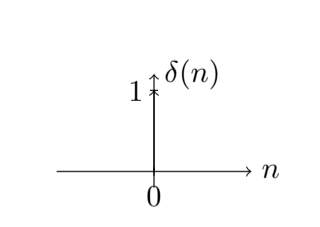
定义一:单位脉冲序列,即$ n=0 $时刻信号强度为$ 1 $,其他时刻信号强度为$ 0 $,可以用符号$ \delta(n) $表示,其中$ \delta $表示脉冲,$ n $表示时刻,即:
$$\delta(n)=\left\{ \begin{array}{rcl} 1,&n=0\\ 0,&n\neq0 \end{array} \right. $$
其函数图像如下图:
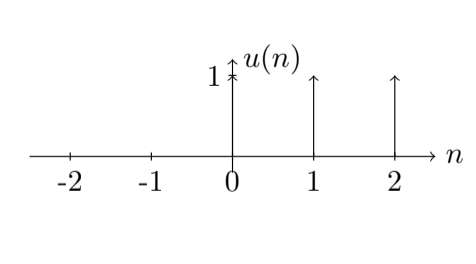
定义二:单位阶跃序列,即$ n \geq 0 $时,信号强度为$ 1 $;$ n<0 $时,信号强度为$ 0 $,可以用$ u(n) $表示,其中$ u $表示阶跃,即:
$$u(n)= \left\{ \begin{array}{rcl} 1,&n\geq0\\ 0,&n<0 \end{array} \right. $$
其函数图像如下图:
易知:
$$ u(k)=\sum_{i=0}^{k}\limits \delta(k-i) $$ $$ \delta(k)=u(k)-u(k-1) $$
Part II
定义三:已知定义在$ (-\infty,+\infty) $上的两个时间序列$ f_{1}(k) $、$ f_{2}(k) $,定义
$$ f(k)=\sum_{i=-\infty}^{\infty}\limits f_{1}(i)f_{2}(k-i) $$
为$ f_{1}(k) $与$ f_{2}(k) $的 卷积和,记为
$$ f(k)=f_{1}(k)*f_{2}(k) $$
注意:求和是在虚变量$ i $下进行的,结果仍为$ k $的函数。
定义四:若对时间序列$ f_{1}(k) $有:当$ k<0 $时,有$ f_{1}(k)=0 $,则称$ f_{1}(k) $为 因果序列。
显然,若$ f_{1}(k) $为因果序列,则有
$$ f_{1}(k)*f_{2}(k)=\sum_{i=0}^{\infty}\limits f_{1}(i)f_{2}(k-i) $$
若$ f_{2}(k) $为因果序列,则有
$$ f_{1}(k)*f_{2}(k)=\sum_{i=-\infty}^{k}\limits f_{1}(i)f_{2}(k-i) $$
如果$ f_{1}(k) $和$ f_{2}(k) $均为因果序列,即$ f_{1}(k)=f_{2}(k)=0, k<0 $,则
$$ f_{1}(k)*f_{2}(k)=[\sum_{i=0}^{k}\limits f_{1}(i)f_{2}(k-i)]u(k) $$
性质 1:任意序列$ x(n) $可表示为$ \delta(n) $的加权移位之线性组合,即
$$ x(n)=…x(-1)\delta(n+1)+x(0)\delta(n)+x(1)\delta(n-1)+…x(m)\delta(n-m)+…=\sum_{m=-\infty}^{\infty}\limits x(n)\delta(n-m)=x(n)*\delta(n) $$
性质 2(交换律):
$$ x_{1}(n)*x_{2}(n)=x_{2}(n)*x_{1}(n) $$
证明:$ x_{1}(n)*x_{2}(n)=\sum_{m=-\infty}^{\infty}\limits x_{1}(m)x_{2}(n-m) $,令$ m=n-k $,则有
$$ \sum_{m=-\infty}^{\infty}\limits x_{1}(m)x_{2}(n-m)=\sum_{k=-\infty}^{\infty}\limits x_{1}(n-k)_{2} (k)=x_{2}(n)*x_{1}(n) $$
性质 3(结合律):
$$ x_{1}(n)*[x_{2}(n) *x_{3}(n) ]=[x_{1}(n)*x_{2}(n)]*x_{3}(n) $$
性质 4(分配律):
$$ x_{1}(n)*[x_{2}(n)+x_{3}(n)]=x_{1}(n)*x_{2}(n)+x_{1}(n)*x_{3}(n) $$
性质 5:
$$ x(n)*u(n)=\sum_{i=-\infty}^{n}\limits x(n) $$
性质 6:
$$ f_{1}(k-k_{1})*f_{2}(k-k_{2})=f_{1}(k-k_{1}-k_{2})*f_{2}(k) $$
例 1:已知$ x(n)= \alpha^n u(n) (0 < \alpha < 1) $,$ \quad h(n)=u(n) $, 求卷积$ y(n)=x(n)*h(n) $。
解:$ y(n)=x(n)*h(n)=\sum_{m=-\infty}^{\infty}\limits \alpha^m u(m)u(n-m) $,
考虑$ x(n) $、$ h(n) $皆为因果序列,有
$$ y(n)=(\sum_{m=0}^{n}\limits \alpha^m)u(n)=\dfrac{1-\alpha^{n+1}}{1-\alpha} $$
当$ n\rightarrow\infty $时,$ y(n)=\dfrac{1}{1-\alpha}u(n) $。
例 2:求$ u(k)*u(k) $。
解:$ u(k)*u(k)=\sum_{i=-\infty}^{\infty}\limits u(i)u(k-i)=(\sum_{i=0}^{k}\limits 1)u(k)=(k+1)u(k) $
试卷问题
1.试证明性质 3 ~ 性质 6。
2.已知$ f_{1}(k)=1.5\delta(k+1)+\delta(k)+1.5\delta(k-1)+2\delta(k-2) $,$ f_{2}(k)=u(k)-u(k-3) $。
试画出$ f_{1}(k) $和$ f_{2}(k) $的图像,并求出$ f_{1}(k)*f_{2}(k) $;作出$ f_{1}(k)*f_{2}(k) $的图像。
3.
(1) $ f(k)=a^ku(k) $,$ h(k)=b^ku(k) $,求$ f(k)*h(k) $;
(2) 求$ a^ku(k)*u(k-4) $;
(3) 求$ u(k-3)*u(k-4) $;
(4) 求$ (0.5)^ku(k)*1 $。
4.已知$ x_{1}(n)=n[u(n)-u(n-6)] $,$ x_{2}(n)=u(n+6)-u(n+1) $,求$ y(n)=x_{1}(n)*x_{2}(n) $。
参考答案
1.略
2.略
3.
(1) $ y(k)= \left\{ \begin{array}{rcl} b^k\dfrac{1-\left(\dfrac{a}{b}\right)^{k+1}}{1-\dfrac{a}{b}}u(k),&a\neq b\\ b^k(k+1)u(k),&a=b \end{array} \right. $
(2) $ y(k)= \left\{ \begin{array}{rcl} \dfrac{1-a^{k-3}}{1-a}u(k-4),&a\neq 1\\ (k-3)u(k-4),&a=1 \end{array} \right. $
(3) $ y (k)= (k-6) u (k-7) $
(4) $ y (k)=2 $
4.
$ y (n)=\dfrac{1}{2} (n+6) (n+7)[u (n+6)-u(n)]+15[u (n)-u (n-5)]-\dfrac{1}{2} (n+1) (n+2)[u (n+1)-u (n-5)] $
