未来技术学院 2024 级选拔考试(数学)参考答案
答案说明
- 未来技术学院未公开发布试卷内容,回忆版试卷内容请浏览往届老生整理的词条:未来技术学院 2024 年选拔考试(数学) ;
- 未来技术学院未公开发布试卷标准答案,本词条内容为往届老生整理的参考答案,无法保证答案的完全准确性与最优性,仅供学习参考;
- 欢迎指出本套答案的不足点,或提供更好的解题思路;
参考答案
一.
1.1
$ d_1(x,y)=(x-y)^2=x^2+y^2-2xy $
$ d_1(x,z)+d_1(z,y)=(x-z)^2+(z-y)^2=x^2+y^2+2z^2-2xz-2zy $
$ d_1(x,y)-[d_1(x,z)+d_1(z,y)]=2xz+2zy-2xy-2z^2 $
不妨设$ y=0 \Rightarrow 2xz-2z^2=2z(x-z) $
若满足性质 D,则$ 2z(x-z) \leq 0 $恒成立,与题设矛盾
$ \Rightarrow $不满足
1.2
$ d_2(x,y)=|x^2-y^2| $
$ d_2(x,z)+d_2(z,y)=|x^2-z^2|+|z^2-y^2|\ge|(x^2-z^2)+(z^2-y^2)|=|x^2-y^2| $
$ \Rightarrow $ 满足
1.3
$ d_3(x,y)=|x-2y| $
$ d_3(y,x)=|y-2x| $,显然$ d_3(x,y) $不恒等于$ d_3(y,x) $
$\Rightarrow $不满足
1.4
$ d_4(x,y)=|x-y|+|y| $
$ d_4(y,x)=|y-x|+|x| $,显然$ d_4(x,y) $不恒等于$ d_4(y,x) $
$ \Rightarrow $不满足
二.
证明:
$ p \ne q $时,$ d(p,q)=1>0 $;$ p=q $时$ d(p,q)=0 $
$ \Rightarrow $满足$ D_1 $
$ p \ne q $时,$ d(p,q)=d(q,p)=1 $
$ p=q $时,$ d(p,q)=d(q,p)=0 $
$ \Rightarrow $满足$ D_2 $
$ p=q $时,$ d(p,q)=0 \le d(p,x)+d(x,q) $,显然成立
$p \ne q $时,$ d(p,q)=1 $,对于$ d(p,x) $与$ d(x,q) $,显然不存在$ x $使得$ p=x $与$ x=q $同时成立
$ \Rightarrow d(p,x)+d(x,q)\ge 1 $
$ \Rightarrow $ 满足$ D_3 \Rightarrow $满足性质 D
① 集合开集 $ \Rightarrow $集合每个点均为内点
当$ r<1 $时,$ N_r(p)=\{q\}|_{p=q}=\{p\} $
因此,对于$ p \in E $,都存在$ r<1 $使得$ N_r(p)=\{p\} $完全包含于 $ E $
$ \Rightarrow $包含$ p $的集合即为开集,由于$ p $在$ X $内不失一般性
$\Rightarrow $所有非空子集都满足(可将其中任意元素视为$ p $)
② 集合闭集 $\Rightarrow $集合每个极限点都在集合中
对于任意$ p \in X $,当$ r<1 $时,$ N_r(p)=\{p\} $恒成立
因此对于$ p $,其$ r<1 $的所有邻域中都仅有$ p=q $一个元素,这与$ p\ne q$矛盾
因此不存在极限点$ \Rightarrow $所有非空子集都满足
三.
3.1
解:(结合图 1)
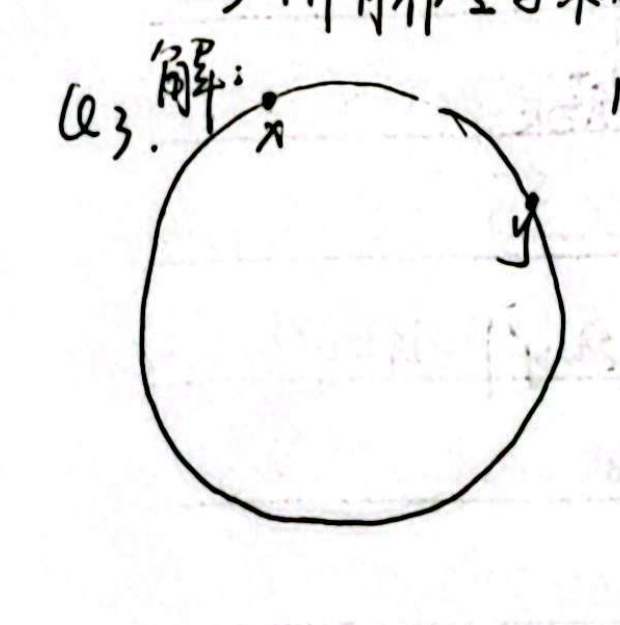
(图片来源:彭宇阳)
① 当且仅当$ x $与$ y $重合时,$ d(x,y)=0 $,否则$ d(x,y)>0 $(因为弧长非负值),满足$ D_1 $
② 显然由$ x $到$ y $之间的劣弧与由$ y $到$ x $的劣弧为同一段弧 $ \Rightarrow d(x,y)=d(y,x) $,满足$ D_2 $
③ 当$ z $位于$ x,y $之间的劣弧上时,$d(x,y)=d(x,z)+d(z,y)$
反之必定存在$ d(x,z) $或者$ d(z,y) $大于$ d(x,y) $
$ \Rightarrow d(x,y) < d(x,z)+d(z,y) $
$ \Rightarrow d(x,y) \le d(x,z)+d(z,y) $,满足 $ D_3 $
$ \Rightarrow $满足性质 D
下证:$ \rho(x,y)\le d(x,y) \le \frac{\pi}{2}\rho (x,y) $(结合图 2)
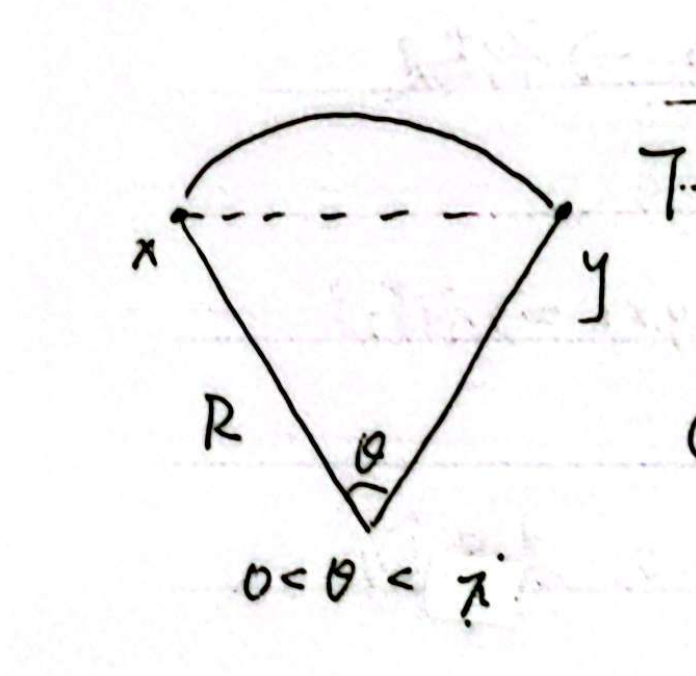
(图片来源:彭宇阳)
① 当$ x=y $时,等式成立
② 当$ x \ne y $时,$ \rho(x,y)=2Rsin\frac{\theta}{2} $,$ d(x,y)=R\theta $
$ d(x,y)-\rho (x,y)=R(\theta-2sin\frac{\theta}{2})=f(\theta) $,($ f(0)=0 $)
$ f'(\theta)=1-cos\theta \ge0 \Rightarrow f(\theta)\ge 0 \Rightarrow d(x,y) \ge \rho (x,y) $
$ d(x,y)-\frac{\pi}{2}\rho(x,y)=R(\theta-\pi sin\frac{\theta}{2})=g(\theta) $,($ g(0)=0 $)
$ g'(\theta)=1-\pi cos\theta (0<\theta<\pi) \Rightarrow g(\theta) $先减小后增大
又$ g(\pi)=0\Rightarrow g(\theta)\le0 \Rightarrow d(x,y)\le \frac{\pi}{2} \rho (x,y) $
3.2
对于任意$ x,y $可取过$ x,y $两点的大圆,便回到了二维问题上
同理可知满足性质 D
下证:$ \rho(x,y)\le d(x,y) \le \frac{\pi}{2}\rho(x,y) $
① $ x=y $时,等式成立
② $ x\ne y $时,不妨假设该圆的圆心为$ (0,0,0) $,半径为 $ R $
$ x=(x_1,x_2,x_3)$,$y=(y_1,y_2,y_3) $
$ \Rightarrow \rho(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}=\sqrt{2R^2-2(x_1y_1+x_2y_2+x_3y_3)} $
$ cos<\vec {OX},\vec {OY}>=\frac{x_1y_1+x_2y_2+x_3y_3}{R^2} $
$ d(x,y)=Rarccos(\frac{x_1y_1+x_2y_2+x_3y_3}{R^2}) $
设$ u=x_1y_1+x_2y_2+x_3y_3 $,($-R^2 \le u \le R^2$)
$ f(u)=d(x,y)-\rho(x,y)=Rarccos\frac{u}{R^2}-\sqrt{2R^2-2u} $
$ f'(u)=R\cdot [-\frac{1}{\sqrt{1-(\frac{u}{R^2})^2}}]\cdot \frac{1}{R^2}-\frac{1}{2\sqrt{2R^2-2u}}(-2) $
$ =\frac{1}{\sqrt{2R^2-2u}}-\frac{1}{\sqrt{R^2-\frac{u^2}{R^2}}} $
$ =\frac{(R^2-\frac{u^2}{R^2})-(2R^2-2u)}{\sqrt{(2R^2-2u)(R^2-\frac{u^2}{R^2})}(\sqrt{R^2-\frac{u^2}{R^2}}+\sqrt{2R^2-2u})} <0 $
又$ f(R^2)=0 \Rightarrow f(u)\ge 0 \Rightarrow d(x,y)\ge \rho(x,y) $
$ g(u)=d(x,y)-\frac{\pi}{2}\rho(x,y) \Rightarrow g'(u)=\frac{\pi}{2\sqrt{2R^2-2u}}-\frac{1}{\sqrt{R^2-\frac{u^2}{R^2}}} \Rightarrow$ $ g(u) $先减后增
$ g(R^2)=0 $,$ g(-R^2)=0 \Rightarrow g(u) \le 0 \Rightarrow d(x,y)\le \frac{\pi}{2}\rho(x,y) $
