数学学院求是数学班 2019 级选拔考试
根据阅读材料,完成后面的五道题.
阅读材料
定义1 偏序集$P$是指一个集合, 其中定义了一个二元关系 $\leq$(有时记做 $\leq_{P}$)满足:
-
自反性: $x \leq x$,
-
反对称性:若 $x \leq y$ 且 $y \leq x$, 则 $x=y$,
- 传递性:若 $x \leq y$ 且 $y \leq z$, 则 $x \leq z$. 和普通的记号一致, 如果 $x \leq y$ 且 $x \neq y$, 则记为 $x < y$ . 如果 $x \leq y$ 或者 $y \leq x$, 则称 $x$与 $y$ 可比较, 否则称为不可比较.
列出偏序集中所有的 $\leq$ 关系或 $ < $ 关系,是一种表示偏序集的方法.例如:我们定义三元集 $\{1,2,3\}$ 中的二元关系为 $\{1 \leq 1,2 \leq 2,3 \leq 3\}$, 它满足上面的三条 性质,因此构成一个偏序集.又如令 $\mathbb{R}$ 表示所有实数构成的集合, 在其中定义二元关系 $a \leq b$ 当且仅当作为数时有 $a \leq b$, 则 $\mathbb{R}$ 构成一个偏序集.
表示偏序集的另一种方法是给出一部分二元关系,由此可以决定出所有的二元关系.为此, 我们首先引入区间和覆盖的概念.假设 $x \leq y$, 则称集 合 $\{z: x \leq z \leq y\}$ 为区间, 记为 $[x, y]$ .在组合数学中, 我们经常讨论的偏序集 满足局部有限性, 即任意的 $x \leq y$, 区间 $[x, y]$ 为有限集,我们称这样的偏序集为局部有限偏序集. 如果 $x < y$ 且 $[x, y]=\{x, y\}$, 则称 $y$ 覆盖 $x$, 记为 $x \lessdot y$ . 对于 局部有限集合, 我们如果给出了所有的覆盖关系,则利用传递性就可以得到所有的偏序关系:
$$\{(x, y): x \leq y\}=\left\{(x, y) \mid \text { 存在 } r \geq 0 \text { 和 } x_{0}=x, x_{1},\right. \cdots, x_{r}=y, \text { 使得 } \left.x_{0} \lessdot x_{1} \lessdot \cdots \lessdot x_{r}\right\}.$$
我们可以用图形表示偏序关系:如果 $y$ 覆盖 $x$, 则我们将 $y$ 放在 $x$ 上面, 并且 在它们中间连一条线.这样得到的图形称为Hasse图.例如
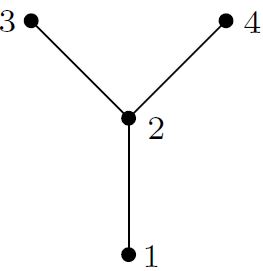
表示集合 $\{1,2,3,4\}$ 上的覆盖关系为 $\{1 \lessdot 2,2 \lessdot 3,2 \lessdot 4\}$, 从而其偏序关系为 $$ \{1<2,1<3,1<4,2<3,2<4\}. $$
下面我们来看一些偏序集的例子:
例一:$n$. 元素为 $[n]=\{1,2, \ldots, n\}, x \leq y$ 就是数的小于等于关系.其中任意两 个元素是可比较的.
例二:$B_{n}$. 其元素为 $[n]$ 的所有子集, $X \leq Y$ 定义为 $X \subseteq Y$ .
例三:$D_{n}$. 其元素为 $n$ 的所有正因子, $i \leq j$ 定义为 $j$ 能被i整除.
例四:$\Pi_{n}$.其元素为 $[n]$ 的所有划分, 即将 $[n]$ 分成若干个互不相交的子集(这些子集称为块).例如 $\{\{1,2\},\{3\},\{4\}\}$ 为 $[4]$ 的一个划分.定义两个划分 $\pi \leq \sigma$ 当且 仅当 $i, j$ 在 $\pi$ 的同一个块中时,必然有 $i, j$ 在 $\sigma$ 的同一个块中.我们称 $\pi$ 为 $\sigma$ 的加细. 例如划分 $\{\{1,2\},\{3\},\{4\}\}$ 为 $\{\{1,2\},\{3,4\}\}$ 的加细.
称偏序集 $P$ 和 $Q$ 同构,如果存在一个从 $P$ 到 $Q$ 的一一映射$f$, 使得 $x \leq_{P}y \Leftrightarrow f(x) \leq_{Q} f(y)$.
设 $P$ 为一个偏序集, $C$ 为其子集.如果 $C$ 中任意两个元素可以比较,则 称 $C$ 为链, 链中元素的个数称为该链的长度. $P$ 中的链 $C$ 称为饱和的,如果不存在 $C$ 之外的元素 $z$ 使得 $C$ 添加 $z$ 后仍然构成链.如果一个偏序集所有的饱和链的长度相等,则称之为分次偏序集.
测试题(每题20分,满分100分)
一. 列出所有以 $1,2,3$ 为元素的偏序集.
二. 画出 $D_{12}$ 和 $\Pi_{3}$ 的Hasse图.
三. 给出 $B_{n}$ 中覆盖 $\{1,2, \ldots, k\}$ 的元素的个数,对一般的子集结论如何?
四. 画出所有含三个元素的不同构的偏序集对应的Hasse图.
五. 设 $P$ 是一个具有最大元(大于所有其他元素的元素)的有限偏序集. 证明: $P$ 为分次偏序集当且仅当存在映射 $\rho: P \mapsto \mathbb{N}=\{0,1,2, \ldots\}$, 使得
- 对任意的极小元 $x, \rho(x)=0$.
- 若 $x \lessdot y$, 则 $\rho(y)=\rho(x)+1$.
